Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.
Symbol Value
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, 2 is written as II in Roman numeral, just two ones added together. 12 is written as XII, which is simply X + II. The number 27 is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:
I can be placed before V (5) and X (10) to make 4 and 9.
X can be placed before L (50) and C (100) to make 40 and 90.
C can be placed before D (500) and M (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
Example 1:
Input: s = "III"
Output: 3
Explanation: III = 3.
Example 2:
Input: s = "LVIII"
Output: 58
Explanation: L = 50, V= 5, III = 3.
Example 3:
Input: s = "MCMXCIV"
Output: 1994
Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
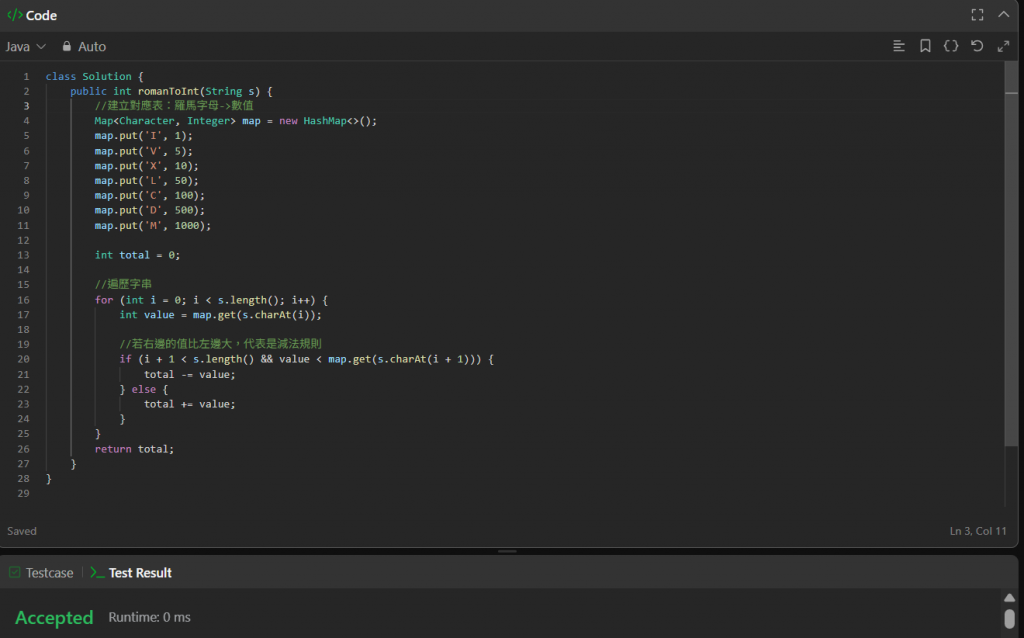
解題思路
1.建立字母對應表
將每個羅馬符號對應到它的整數值。
2.逐字遍歷字串
每次讀取當前字母的數值，並與下一個字母比較：
若當前值<下一個值，表示是減法情況，此時要減去當前值。
否則就是正常加法，直接加上當前值。
3.為什麼這樣可行？
羅馬數字的特殊在於只可能連續出現一次減法，例如：
IX（9）=-1+10
MCMXCIV（1994）=1000-100+1000-10+100-1+5
這樣用加減法即可得到正確結果。
4.處理到最後一位時
若沒有右邊字母可比較，就直接加上該數值。